
Solve a logarithmic equation interactively using this step-by-step example. So the solution to the original problem is x = 3. However, due to the restrictions placed on the original equation, that is, x > 2, only solutions found in the solid region are valid for the original problem.

Graphed on the right is the function x 2 + 11 x − 42, with the two roots shown. Our math solver supports basic math, pre-algebra, algebra, trigonometry, calculus and more.
#Solving logs free
X + 14 ⋅ x − 3 = 0, so x = − 14 or x = 3 Solve your math problems using our free math solver with step-by-step solutions. Inverting the logarithm by raising 16 to both sides gives: This means the domain of the function y = log 16 x + 13 + log 16 x − 2 is the set of all numbers satisfying x > 2. Use the theorem above that we just proved.
#Solving logs how to
In solving exponential equations, the following theorem is often useful: Here is how to solve exponential equations: Manage the equation using the rule of exponents and some handy theorems in algebra. These rules help us a lot in solving these type of equations. Note that since we can only take the logarithm of positive numbers, the domain of the left-hand side function is the set of all numbers satisfying both x + 13 > 0 and x − 2 > 0, or equivalently x > − 13 and x > 2. To solve exponential equations, we need to consider the rule of exponents. The solution to the problem is their intersection. Use the (reverse of the) product rule for logarithms:Įach side of the above equation is graphed to the right. Suppose we want to find the solutions to this equation:


The product rule for logarithms requires that all the logarithms appearing in the rule be properly defined. As a simple illustration, observe that the domain of the function y = log 3 x 2 is x ≠ 0, while the domain of y = 2 log 3 x is x > 0. As we will see in the examples below, algebraic manipulations of expressions involving logarithms can easily lead to "solutions" which are not valid because of this domain restriction. Ĭaution: When solving equations involving logarithms, it is very important to keep in mind that the domain of a logarithm function is the positive numbers. So, there are two solutions: x = 2 4 = 16 and x = 2 − 4 = 1 16. Taking the square roots of both sides gives log 2 x = ± 4. Substituting this into log 4 x ⋅ log 2 x = 8 and cross-multiplying by 2, we get log 2 x ⋅ log 2 x = log 2 x 2 = 16. Next, using the change of base rule, we have log 4 x = log 2 x log 2 4 = log 2 x 2. Solution: First, note that by the power rule log 2 x 2 = 2 log 2 x, so the original equation reduces to log 4 x ⋅ log 2 x = 8. If the equation can be manipulated into the form log b x = y (that is, involving just a single logarithm) then x = b y.
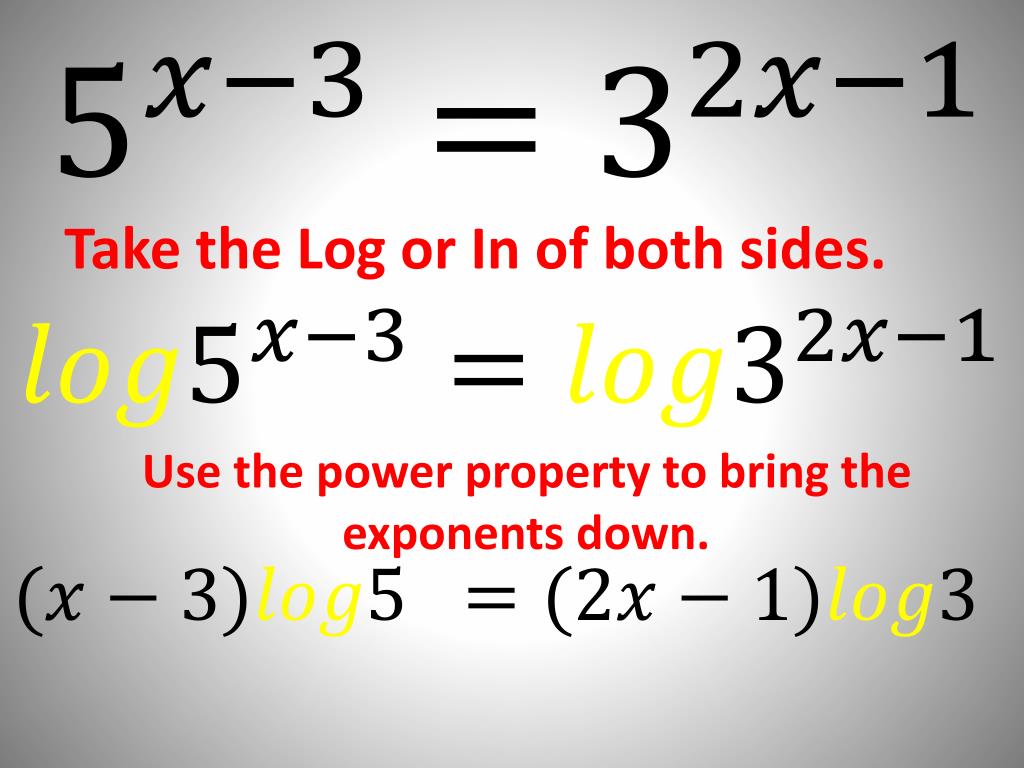
If an equation with logarithms can be solved using algebraic techniques, then those techniques will generally involve the product, quotient, and power rules of logarithms-applied in either direction-as well as examining the problem for common bases. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License. We recommend using aĪuthors: Lynn Marecek, Andrea Honeycutt Mathis Use the information below to generate a citation. Then you must include on every digital page view the following attribution: If you are redistributing all or part of this book in a digital format, Then you must include on every physical page the following attribution: Take log10 on both sides separating the power(s). (1) lnx 3 (2) log(3x 2) 2 (3) 2logx log2+log(3x 4) (4) logx+log(x 1) log(4x). In order to successfully solve logarithmic equations, the three basic steps must firstly be followed: 1. If you are redistributing all or part of this book in a print format, Solve the following logarithmic equations. Want to cite, share, or modify this book? This book uses the


 0 kommentar(er)
0 kommentar(er)
